基于 Metal 的并行来计算实现高斯模糊
一直想自己实现一下高斯模糊效果，最近总算完成一个性能不算太差的实现。
高斯模糊
图片模糊的原理和图片马赛克原理类似，一般情况下，如何将一张图展示在计算机屏幕上，在光栅化的渲染管线算法中，我们只需要每个像素点展示对应这个像素点（x，y）的颜色即可。对应到着色器上的代码是：
// 其中 texture 为纹理，textureSampler 为参数， st 为像素点纹理坐标；
float4 textureColor = texture.sample(textureSampler, st);
return textureColor;
如何将图片加上马赛克？假设我们有一张 100100 大小的图，马赛克 size 是 4，那么我们可以将图分割成 2525 个区域，每块区域里的 16 个像素点都显示成一样的颜色即可，对应代码可以这样写：
int width = 100;
int d = 4;
int x = st.x*100;
int y = st.y*100;
// 取每个区域里左上角的颜色
int newX = (x/d) * d;
int newY = (y/d) * d;
float2 newST = float2(newX, newY);
float4 textureColor = texture.sample(textureSampler, newST);
return textureColor;
接下来，怎么将图片模糊化？假设依然是一张 100100 大小的图，模糊半径是 4，此时我们可以这样做，对每个位置的点（x,y），以该点为中心。取（x-4,y-4）到 (x+4,y+4) 这样一个范围内所有的 99 个点的颜色平均值即可，对应代码差不多可以这样写：
int size = 9;
float r = 0;
float g = 0;
float b = 0;
for (int i=0; i < size; i++){
for (int j=0; j < size; j++){
float weight = 1.0/81.0;
Color clr = inA[w*(ii + i - br) + (jj + j - br)];
r = r+ clr.r * weight;
g = g+ clr.g * weight;
b = b+ clr.b * weight;
}
}
float4 textureColor = float4(r, g, b, 1.0);
return textureColor;
这样处理后，每个像素点的颜色都变得和周围的颜色相关而丢失了自己的细节，图片整体颜色变得平滑，变得“模糊”。
相比于上述平均模糊算法，高斯模糊则做了进一步处理，每个点颜色不再简单取周围颜色的平均值，而是加权平均值。因为一般认为图像是连续的，靠近目标点关系月密切，需要分配更大的权值。而周围点的权值，则使用二维正态分布（又名二维高斯分布）来计算，通过查询某科，正态状态分布公式为：
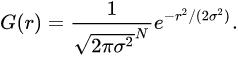（N = 2）
卷积矩阵计算
卷积矩阵就是上面提到的权值数组，假设我们要处理一张 600*900 的图，做半径为3的高斯模糊，那么根据上面二维正态分布公式，可这样得到权值数组：
- (float)getWeightWithR: (int)br x:(int) x y:(int) y {
float pi = 3.14159265359;
float e = 2.718281828459;
float sigma = (br*2+1)/2; // 标准方差
float weight = (1/(2*pi*sigma*sigma))*pow(e,((-(x*x+y*y))/((2*sigma)*(sigma))));
return weight;
}
再做一下归一化：
// br：模糊半径
- (void) getWeightMatrixWithR: (int)br inArr:(float *)weightArr {
int size = br*2+1;
float sum = 0;
for (int i=0;i < size;i++){
for (int j=0;j < size;j++){
int index = i*size + j;
float weight = [self getWeightWithR:br x: j-br y: br-i];
// 这里偏移了 4 个单位，因为前面 4 个值另外做别的使用
weightArr[index + 4] = weight;
sum += weight;
}
}
for (int i=0;i < size;i++){
for (int j=0;j < size;j++){
int index = i*size + j;
weightArr[index + 4]/=sum;
}
}
}
如此则得到加权数组，存与数组 weightArr 中。
图片数据读取
在 iOS 里使用 CoreGraph 获取图片数据，并做处理，可用如下方法：
CGImageRef cgimage = image.CGImage;
size_t width = CGImageGetWidth(cgimage); // 图片宽度
size_t height = CGImageGetHeight(cgimage); // 图片高度
unsigned char *data = calloc(width * height * 4, sizeof(unsigned char)); // 取图片首地址
size_t bitsPerComponent = 8; // r g b a 每个component bits数目
size_t bytesPerRow = width * 4; // 一张图片每行字节数目 (每个像素点包含r g b a 四个字节)
CGColorSpaceRef space = CGColorSpaceCreateDeviceRGB(); // 创建rgb颜色空间
CGContextRef context =
CGBitmapContextCreate(data,
width,
height,
bitsPerComponent,
bytesPerRow,
space,
kCGImageAlphaPremultipliedLast | kCGBitmapByteOrder32Big);
CGContextDrawImage(context, CGRectMake(0, 0, width, height), cgimage);
... 对data的处理...
cgimage = CGBitmapContextCreateImage(context);
return [UIImage imageWithCGImage:cgimage];
其中 data 就是图片的颜色值数组，假设图片大小 600*900，则数组大小为 width * height * 4，数组元素为unsigned char 存值范围（0～255），每4个值为一个像素点的 rgba 值，例如坐标（i , j）处的颜色值为：
size_t pixelIndex = i * width * 4 + j * 4;
unsigned char red = data[pixelIndex];
unsigned char green = data[pixelIndex + 1];
unsigned char blue = data[pixelIndex + 2];
unsigned char alpha = data[pixelIndex + 3];
Metal 并行计算
关于 metal 这里不做多余介绍，苹果介绍（吹）的已经够多了，这里有介绍一下并行计算，Erlang 之父 Joe Armstrong 用一张 5 岁小孩都能看懂的图解释了并发与并行的区别：
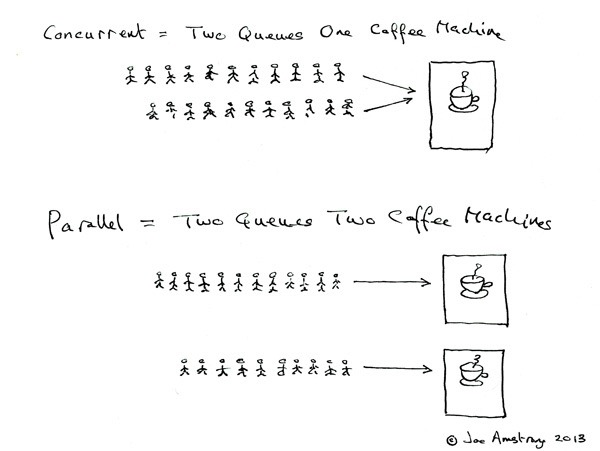
并发就是多个队列交替使用一台咖啡机器，并行就是多个队列同时使用多台咖啡机。这里不难看出并行计算要更快，也不难看出为了做并行计算需要更多的咖啡机（运算器 ALU），而 GPU 则天然适合做并行计算，因为GPU由数量众多的计算单元和超长的流水线组成，适合处理大量的类型统一的数据，事实上目前也有很多 GPU 并行计算的框架，如英伟达的 Cuda，又如本文要用的 Metal
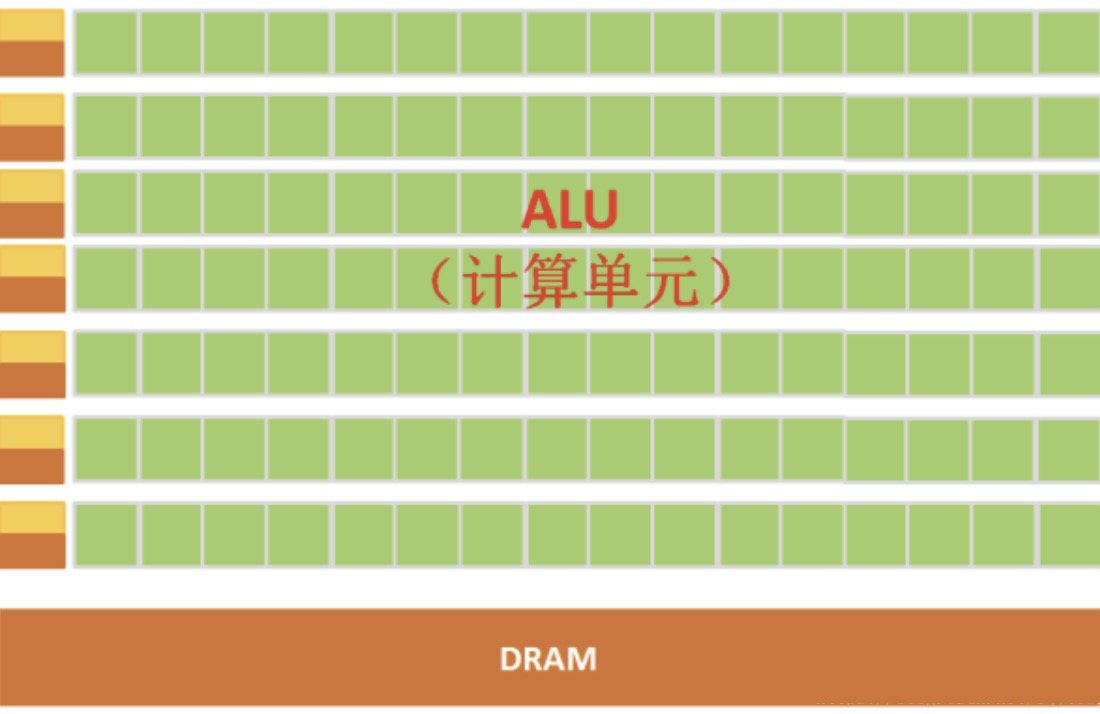
一般来说使用 GPU 做并行计算的过程和把大象装进冰箱一样简单：
- 根据要处理的数据大小，设置对应大小的 GPU 缓存
- 设计 GPU 核函数，来用于处理每个数据单元
- 缓存设置索引绑定，对计算命令进行编码
- 传入数据，提交计算，等待计算结果取回数据
并行计算处理高斯模糊关键代码如下：
- (void) prepareDataWith: (unsigned char *)data CM: (float *)cm width: (size_t)width height:(size_t)height
{
arrayLength = width * height * 4;
bufferSize = arrayLength * sizeof(unsigned char);
_mBufferResult = [_mDevice newBufferWithLength: bufferSize
options: MTLResourceStorageModeShared];
_mBufferA = [_mDevice newBufferWithBytes: data
length: bufferSize
options: MTLResourceStorageModeShared];
_mBufferCM = [_mDevice newBufferWithBytes: cm
length: bufferSize
options: MTLResourceStorageModeShared];
}
其中在 GPU 开辟了3快显存，_mBufferResult 为将要得到的结果，_mBufferA 为传入的图片数据，即上文的提到的 data，_mBufferCM 为夹带参数，里面存储宽高数据、高斯模糊半径、和高斯卷积矩阵。
kenerl 函数如下：
kernel void ppp_arrays(device const Clr* inA, // _mBufferA
device const float* inCM, // _mBufferCM
device Clr* result, // _mBufferResult
uint index [[thread_position_in_grid]])
{
int w = inCM[0];
int h = inCM[1];
int br = inCM[2]; // 模糊半径
int rw = inCM[3]; // 周围边长
int ii = index/w; // 行
int jj = index%w; // 列
// 边缘防越界
if (ii <= rw || ii >= h-rw ||
jj <= rw || jj >= w-rw) {
result[index] = inA[index];
result[index].r = 255;
return;
}
float r = 0;
float g = 0;
float b = 0;
// 在rw为边长的矩形范围内做加权平均
for (int i=0; i < rw; i++){
for (int j=0; j < rw; j++){
float weight = inCM[i+j*rw + 4];
Clr clr = inA[w*(ii + i - br) + (jj + j - br)];
r = r+ clr.r * weight;
g = g+ clr.g * weight;
b = b+ clr.b * weight;
}
}
result[index].r = r;
result[index].g = g;
result[index].b = b;
result[index].a = 255;
}
提交运算得到结果后，深拷贝给 data：
- (unsigned char *) getResult2 {
unsigned char * result = _mBufferResult.contents;
// [self verifyResults];
return result;
}
...
{
MetalAdder* adder = [[MetalAdder alloc] initWithDevice:device];
[adder prepareDataWith: data CM: cmArr width: width height:height];
[adder sendComputeCommand];
unsigned char *r = [adder getResult2];
memcpy(data, r, height * width * 4);
}
修改 data 后，通过 cgimage = CGBitmapContextCreateImage(context) 即可得到最后的 image。
运行结果：
取一张1024*1024大小的图做实验，
原图：
做 size为 8 马赛克后
做半径是 8 边长是17的平均模糊：
做半径是 8 边长是17的高斯模糊（Metal 耗时 100ms）：
下图为 1024*1024，不同半径下的处理耗时：
| 模糊半径 r | 需要卷积顶点数（2r+1）(2*r+1) | 耗时(单位：ms) |
|---|---|---|
| 2 | 25 | 70 |
| 4 | 81 | 91.683984 |
| 8 | 289 | 89.900970 |
| 16 | 1089 | 120.525956 |
| 32 | 4225 | 179.502964 |
| 64 | 16641 | 400.424004 |
数据含义，例如 10241024的图，需要处理计算大约 10241024 个点，在半径为 8 时，每个点要循环附近
17*17 = 289 个点做叠加运算，总共约做 3亿 次计算，耗时 89.9ms。当半径是 64 时，计算 17 亿次，耗时 400 ms
本文的代码可以在 首页->代码仓库->demo 里获取
既已览卷至此，何不品评一二：